При ведении геодезических работ, разведке нефтяных и газовых месторождений, поисках других полезных ископаемых и т.п. часто возникает следующая задача: на плоскости, касательной к земной поверхности, имеются точки, в которых заданы значения функции. Требуется построить гладкую функцию, проходящую через эти точки. Из всего множества удовлетворяющих этому условию функций мы выбираем ту, которая в наибольшей степени соответствует реальной физической поверхности, обладающей рядом физических свойств таких, например, как: сопротивление к изгибам, растяжению, или стремление занимать минимальную площадь. Такие условия, применённые к точкам, разбросанным на плоскости, приводят при подборе функции к сложной задаче многомерной нелинейной оптимизации.

Многие эффективные методы решения этой задачи основываются на построении сеток, в узлах которых находятся опорные точки. Наибольшее распространение получили прямоугольные сетки. Альтернативой может служить метод, базирующийся на создании на поверхности сетки непересекающихся треугольников с вершинами в опорных точках. Идея метода заключается в том, что, поскольку треугольник определяется стороной и двумя углами, то, производя геодезические измерения, можно один раз измерить расстояние между двумя точками, а дальше просто двигаться по местности, замерять направления на различные ориентиры и производить соответствующие тригонометрические пересчёты.

К достоинствам последнего подхода можно отнести:

1. Отсутствие единого, произвольно выбранного масштаба для всех данных - размер ячейки сетки автоматически устанавливает предел подробности карты. Триангуляция же опорных точек естественным образом подстраивается под данные. Там где опорные точки разрежены, треугольники крупнее, там, где есть сгущения, - мельче. Число треугольников определяется по формуле Эйлера и не превышает удвоенного числа опорных точек. В правильности этого утверждения можно убедиться, если устремить длину внутреннего ребра к нулю. В итоге мы получим на одно ребро и две вершины меньше.
2. У прямоугольной сетки есть два выделенных направления, никак не согласованные с начальными данными. Имея в качестве реальной по-верхности горный хребет, который тянется наискосок или извилистое русло реки, мы будем вынуждены сильно измельчить сетку, что по-требует значительных вычислительных мощностей и приведёт к образованию не устойчивостей. Использование же триангуляционной сетки позволит построить аппроксимирующую поверхность по нескольким треугольникам - достаточно обозначить гребень и подножие (дно и берега).

Основным же недостатком триангуляционной сетки является сложность программирования. Уже сам процесс построения триангуляционной сетки является нетривиальной задачей.

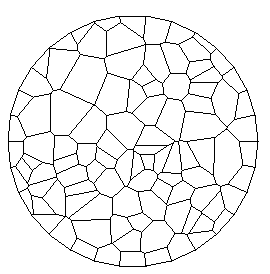
Один из вариантов её построения связан с разбиением плоскости на области Вороного, введённые Г.Ф. Вороным в 1908 году. Смыслом этого разбиения является разграничение плоскости на области, состоящие из точек, объединённых общей ближайшей опорной точкой.

Назовём V_i область Вороного точки i. Если точек только две, то, очевидно, что срединный перпендикуляр к соединяющему их отрезку делит плоскость на две соответствующие области Вороного. В общем случае область Вороного точки i получается как пересечение всех полуплоскостей, содержащих эту точку и ограниченных срединными перпендикулярами к отрезкам, соединяющим i с остальными опорными точками. Поэтому области V_i будут ограничены выпуклой ломанной.

Полученная решётка обладает следующими свойствами:

её рёбра - это отрезки срединных перпендикуляров. Поэтому, если некоторая вершина О области V_b получена пересечением срединных перпендикуляров к отрезкам AB и BC, то она равноудалена от A и от B, от B и C, то есть точка О - это центр описанной окружности треугольника ABC и срединный перпендикуляр к AC тоже проходит через О. Так как Так как О принадлежит V_b , то не существует опорных точек, расположенных к О ближе, чем В, но ОА=ОВ=ОС, поэтому O принадлежит V_a и O принадлежит V_c

Кроме того области Вороного образуют решётку, в каждой вершине которой, в общем положении, сходятся три ребра и три области.

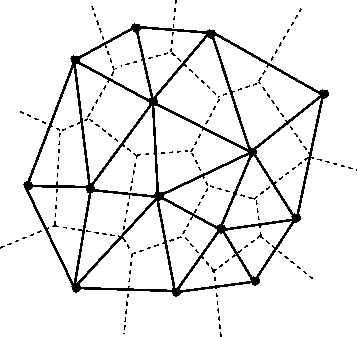
Если соединить между собой точки, области Вороного которых граничат друг с другом, мы получим триангуляцию, причём вершины областей Вороного будут центрами описанных окружностей для полученных треугольников. Такая конструкция называется триангуляцией Делоне.

У неё есть и другие эквивалентные определения. Одно из них характеризует свойство триангуляции Делоне давать локально наиболее правильные треугольники. Звучит оно так: триангуляция будет триангуляцией Делоне тогда и только тогда, когда в любой паре треугольников с общим ребром, в которой это ребро можно перебросить, не нарушая планарность триангуляции, от такой переброски минимальный из шести углов в паре треугольников не увеличится (такая переброска, кстати, носит специальное название - флип). Иными словами, от любой локальной перестройки триангуляции Делоне треугольники становятся более неправильными. Доказательство этого факта следует из другого определения триангуляции Делоне, так называемого кругового критерия.

Для того чтобы триангуляция была триангуляцией Делоне, необходимо и достаточно, чтобы внутри окружности, описанной вокруг любого из треугольников, не лежало больше ни одной вершины триангуляции Делоне.

Доказательство эквивалентности этих трёх определений:

рассмотрим триангуляцию, удовлетворяющую круговому критерию, и возьмём в ней произвольную пару треугольников с общим ребром, допускающую флип. Пусть это будут треугольники ABC и BCD. Если минимальный из углов BAC или BDC, то, очевидно, что он не увеличится при флипе. Если же минимальный угол принадлежит к общей стороне, то пусть это будет, например, угол ABC. Опишем около треугольника ABC окружность. По круговому критерию точка D должна быть вне неё. Пусть ребро AD пересекает окружность в точке E. Тогда углы ABC и AEC рав-ны, так как опираются на одну и ту же дугу, а угол ADC, очевидно, меньше AEC, то есть в любом случае при флипе минимальный угол не увеличится. В обратную сторону доказательство проводиться аналогично. Доказательство эквивалентности кругового критерия определению через области Вороного проводится от обратного: пусть триангуляция Делоне, построенная выше не удовлетворяет критерию и внутрь окружности с центром О, описанной вокруг треугольника АВС, попала вершина D. Как уже было показано, точка О - общая вершина трёх областей Вороного V_b , V_a и V_c.Но раз точка D внутри окружности, она находится ближе к точке О, чем А, В и С. Поэтом О принадлежит V_b, O принадлежит V_a , O принадлежит V_c и их пересечению. Доказательство в обратную сторону аналогично.

При создании алгоритма, автоматизирующего построение триангуляции Делоне, в качестве базового, выбрано было свойство триангуляции Делоне давать локально наиболее правильные треугольники. Это позволило, во-первых, не боятся ошибок, связанных с машинными погрешностями (эта проблема актуальна при определении и ' сшивании ' областей Вороного), во-вторых, получить инкрементный алгоритм, то есть алгоритм, постепенно включающий точки в уже построенную триангуляцию и по определению позволяющий легко реагировать на ситуацию при появлении новых данных и, в третьих, данный алгоритм работает за время, пропорциональное числу (а не квадрату числа - как при работе с областя-ми Вороного) точек.

Ещё одним преимуществом этого алгоритма является простота удаления ранее внесённых и обработанных точек. Простота эта обусловлена таким свойством триангуляции, как независимость её внутри и вне многоугольника. Доказывается это свойство на основании симметрии кругового критерия: если D лежит вне окружности, описанной вокруг BCD, то A лежит вне окружности, описанной вокруг BCD. Это означает, что перестройка триангуляции после удаления из неё точки сводится к триангуля-ции её соседей. В алгоритме эта задача решается созданием локального набора точек, соседних к удалённой, построением триангуляционной сетки на этих точках и добавлением созданных треугольников в глобальную базу.

Подводя итог вышесказанному, можно отметить, что благодаря воз-можности легко вносить и удалять точки из ранее построенной триангуляционной сетке, мы получаем алгоритм, способный работать в реальном времени.

Одной из основных трудностей при использовании инкрементного алгоритма является проблема отыскания того треугольника, в который попала новая точка. Решена эта проблема была следующим образом: вводится вспомогательная очень крупная прямоугольная сетка, в каждую из ячеек которой попадает некоторое число треугольников. Определив, к какой ячейке принадлежит новая точка, локализуются ' подозрительные ' треугольники. Проверяя принадлежность точки к этим треугольникам, либо получаем искомый номер, либо выясняется, что точка лежит вне уже построенной конструкции.

Обработка последнего случая вызывает некоторые трудности, требуется проверить каждую из внешних точек имеющейся триангуляции Делоне на возможность соединения с новой точкой, и последующего образования треугольника. Эту проблему я решил путём исследования отрезка, соединяющего новую точку с рассматриваемой, на предмет пересечения его с каким-либо внешним ребер, имеющейся триангуляции Делоне. Пересечение (или его отсутствие) устанавливается изучением системы линейных уравнений, образованной уравнениями прямых, содержащих вышеупомянутые отрезки.

В случае попадания новой точки в треугольник, ранее построенной триангуляции, происходит ликвидация этого треугольника и появление трёх новых (на базе четырёх точек - новой и трёх вершинах ликвидированного треугольника). Появившиеся треугольники исследуются на воз-можность построения флипов. Преобразованные после флипов треугольники добавляются в разряд исследуемых.

Если говорить о перспективах развития данного алгоритма, то в мои дальнейшие планы по работе в данной области входит оптимизация структуры представления используемых данных в ЭВМ с целью миними-зации времени работы алгоритма, реализация вышеприведённого алгоритма на конкретном языке программирования (работа в этом направлении уже ведётся. В качестве базового выбрана среда программирования -DELPHI), а также непосредственное решение, приводившейся в самом начале задачи построения проходящей через опорные точки гладкой функции.